プロコンに参加した方がいいという天啓を得た気がするので、ほぼ1年ぶり2回目の参加です。

コンテストページ
http://arc036.contest.atcoder.jp

解説スライド

結果と復習

ooxx

A - ぐっすり

普通にやる

B - 山のデータ

最初\(s \lt t \lt u\)と勘違いしてWAもらった。問題文をよく読みましょう。

C - 偶然ジェネレータ

本番では部分点も取れなかった。低能なのでお絵かきしないとわからない。

1でyに+1, 0でyに-1進むと考えると1つの数列は下図のような経路として考えられる。

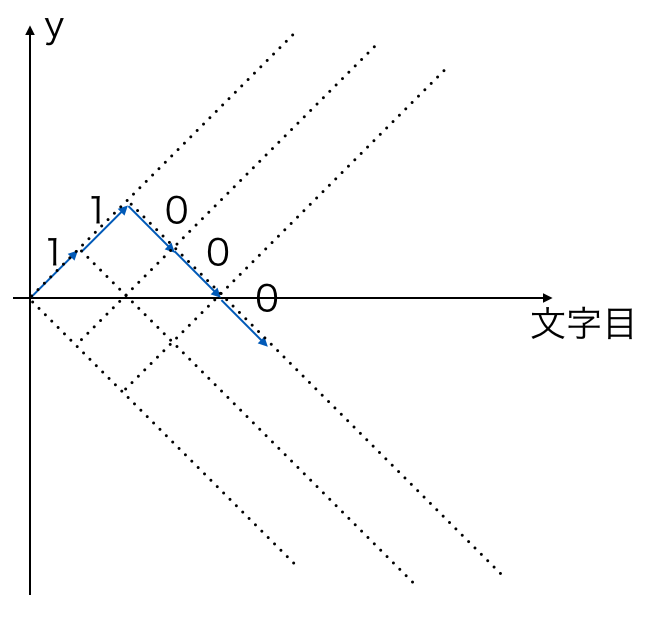
部分列をとったときの0の個数と1の個数の差の最大値は(yの最大値 - yの最小値)なので、それが\(K\)以下となるような経路を数えればいい。通ってきた経路自体は必要のない情報で、

int N, K;
string S;

int solve(int i, int lower, int upper, int current) {
  if(upper - lower > K) return 0;
  if(i == N) return 1;
  switch(S[i]) {
  case '0':
    return solve(i+1, min(lower, current-1), upper, current-1);
  case '1':
    return solve(i+1, lower, max(upper, current+1), current+1);
  case '?':
    return solve(i+1, min(lower, current-1), upper, current-1) +
      solve(i+1, lower, max(upper, current+1), current+1);
  }
  return 0;
}

int main() {
  cin >> N >> K >> S;
  cout << solve(0, 0, 0, 0) << endl;
  return 0;
}

とすれば部分点まではとれる。

上では最大値、最小値、現在位置という値をもっているけれども
今後同じ数列を読み込む際には(iが同じ)最大値と最小値の差とその中での相対位置が共に同じならば、それ以降の列から作れる条件を満たす経路の数は同じなので、それを同一視する。

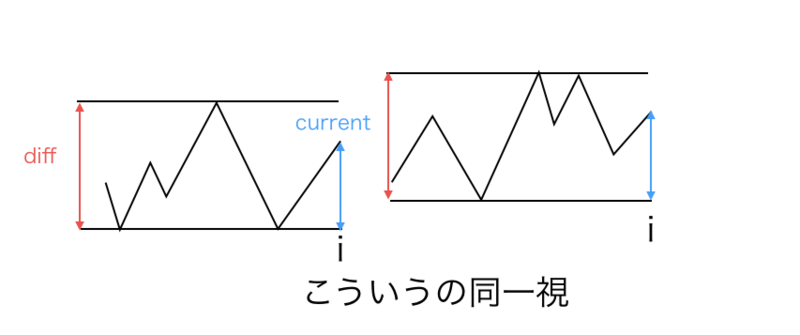
int d = 1000000007;
int N, K;
string S;

int memo[300][300][300];

int solve(int i, int diff, int current) {
  if(diff > K) return 0;
  if(i == N) return 1;
  if(memo[i][diff][current] != -1) return memo[i][diff][current];
  int res = 0;

  if(S[i] != '0') {
    if(current == diff) { // 上に突き抜ける
      res += solve(i+1, diff+1, current+1);
    } else {
      res += solve(i+1, diff, current+1);
    }
  }
  if(S[i] != '1') {
    if(current == 0) { // 下に突き抜ける
      res += solve(i+1, diff+1, 0);
    } else {
      res += solve(i+1, diff, current-1);
    }
  }

  res %= d;
  return memo[i][diff][current] = res;
}

int main() {
  cin >> N >> K >> S;
  memset(memo, -1, sizeof(memo));
  cout << solve(0, 0, 0) << endl;
  return 0;
}

O(N^3)で計算量は余裕だしメモリもギリギリ大丈夫。

振り返ると部分点まではとれてもよかったんじゃないかなという感じ。

D - 偶数メートル

本番中は問題も読まなかった。復習時もこれは前提知識が全然足り無さそうなのですぐに解説を見てしまった。
考察や満点解答が頭良すぎて笑った。

2ノードが同じ連結成分に属するかの判定

Union Findを使う。

Union Find Tree

互いに素な集合(\(A\cap B = \phi \))の集合を表すデータ構造。

• 2要素が同一の集合に属しているかの判定
  
• 集合を併合
  
  

を高速（\(\alpha(n)\)をアッカーマン関数の逆関数として\(O(\alpha(n))\)）に行えるらしい。

2部グラフの判定

未彩色な隣接ノードに別の色を塗っていくDFSで判定する。

感想

元々ほとんど書けないけどC++の書き方をすっかり忘れている。まぁそこが律速になるほどアルゴリズムを分かっていないので特に問題は無いが…。
知らないことが多すぎて、ちゃんと復習しようとすると時間がかかりすぎる。
がんばってこ。